Engineers need to solve Lagrangian systems, and they often undergo a tedious conversion process to convert the system into an ordinary differential equation. For a small system, this approach is possible. However, we must solve large systems.

We use the power of automatic differentiation and the DAETS numerical solver to numerically solve Lagrange systems in natural coordinates.

In our approach, the Lagrange system can be encoded in a form very close to its mathematical description. There is no need to convert it to its ODE or even DAE form, a tedious process that typically involves using cylindrical or spherical coordinates.

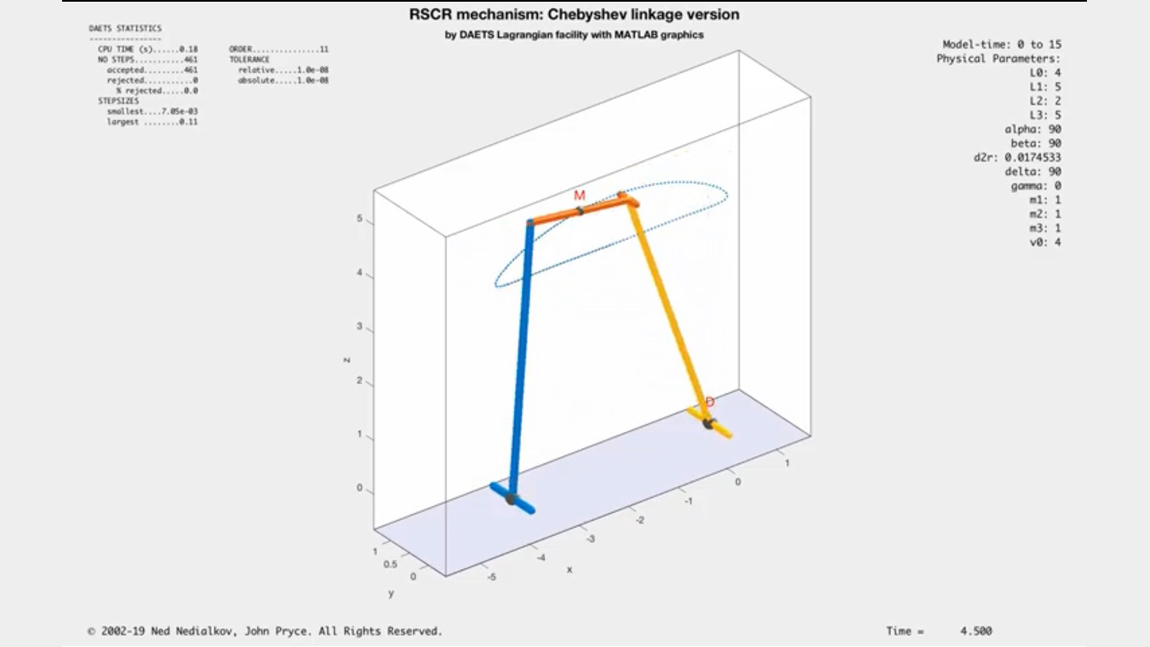
MatLab interface: Graphically represent solving the Lagrange system.

Smarty Pixels brings this caliber of innovation and curiosity to your organization. Ask how the Smarty Pixels can benefit your organization.

Publications

PN2019

J. D. Pryce and N. S. Nedialkov: Data, Lagrangian, Action! Simulating mechanisms direct from a text file. [link]